Pengertian Teorema Norton dan Cara Perhitungannya

Pengertian Teorema Norton dan Cara Perhitungannya – Teorema Norton (Norton Theorem) adalah salah satu Teori atau alat analisis yang dapat digunakan untuk menyerderhanakan suatu rangkaian linear yang rumit menjadi rangkaian yang lebih sederhana. Berbeda dengan Teorema Thevenin yang penyederhanaannya menggunakan sumber tegangan (Voltage Source) ekivalen dengan merangkai resistor ekivalen secara seri, Teorema Norton menyederhanakannya dengan menggunakan sumber Arus (Current Source) ekivalen dan perangkaian resistor ekivalen secara paralel.
Baca juga : Pengertian Teorema Thevenin dan Cara Perhitungannya.

Teorema Norton ini berasal dua orang peneliti yang bernama Hans Ferdinand Mayer dari Siemens & Halske dan Edward Lawry Norton dari Bell Labs. Karena ditemukan oleh dua orang peneliti, Teorema Norton ini juga sering disebut dengan Teorema Mayer – Norton (Mayer – Norton Theorem).

Bunyi Teoreme Norton

Teorema Norton menyatakan bahwa :

Setiap jaringan listrik linear atau rangkaian rumit tertentu dapat digantikan oleh rangkaian sederhana yang hanya terdiri dari sebuah Arus sumber (I_N) dan sebuah Resistor yang diparalelkan (R_N).

Rangkaian pengganti tersebut dinamakan juga dengan Rangkaian Ekivalen Norton.

Cara Menganalisis Rangkaian Linear dengan Perhitungan Teorema Norton

Berikut ini adalah langkah-langkah untuk menganalisis dan menghitung suatu rangkaian linear dengan menggunakan Teorema Norton.

1. Hubung singkat Resistor Beban.
2. Hitung atau ukur arus pada rangkaian hubung singkat tersebut. Arus ini disebut dengan Arus Norton (I_N).
3. Buka Arus Sumber, Hubung singkat Tegangan sumber dan lepaskan Resistor Beban.
4. Hitung atau ukur Resistansi Rangkaian Terbuka. Resistansi ini dinamakan dengan Resistansi Norton (R_N).
5. Gambarkan kembali dengan memasukan nilai arus pada rangkaian yang dihubungsingkat di langkah 2. Rangkaikan Arus sumber dan Resistansi pada Rangkaian terbuka yang dilakukan pada langkah 5 secara paralel. Hubungkan kembali Resistor Beban yang kita lepaskan pada langkah 3. Ini merupakan rangkaian yang telah disederhanakan berdasarkan teorema Norton atau biasanya disebut dengan Rangkaian Ekivalen Norton.
6. Carikan Arus Beban yang mengalir dan Tegangan Beban pada Resistor Beban berdasarkan aturan Pembagi Arus listrik (Current Divider Rule).
   I_L = I_N / (R_N/(R_N+R_L)

Contoh Kasus Perhitungan Teorema Thevenin

Berikut ini adalah contoh kasus untuk menganalisis Rangkaian Linear dengan menggunakan Teorema Norton dengan mengikuti langkah-langkah diatas.

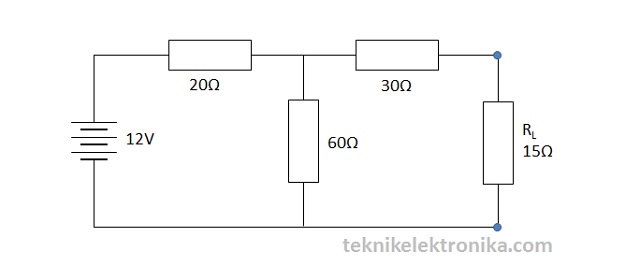
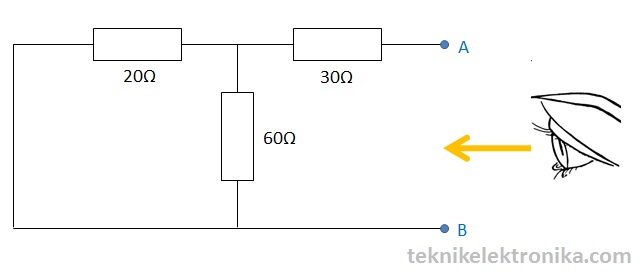
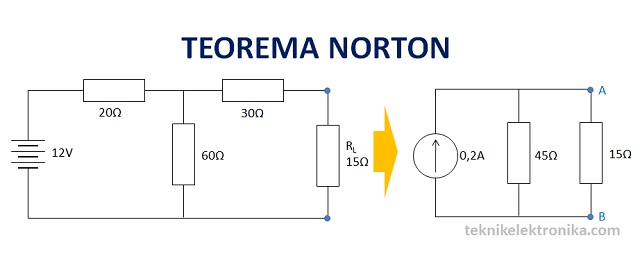
Pada gambar dibawah ini, carikan Nilai Resistansi Norton (R_N) dan Arus Norton (I_N) serta Tegangan Beban (V_L) pada Resistor Beban (R_L) dengan menggunakan Teorema Norton.

Penyelesaian :

Langkah 1.

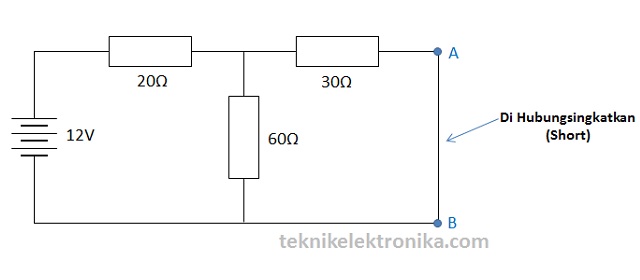
Hubung singkat Resistor beban 15Ω seperti pada gambar berikut ini :

Langkah 2.

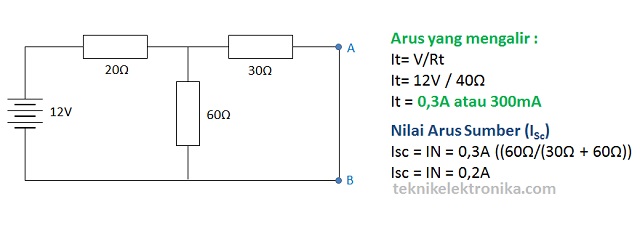
Hitung atau ukur arus rangkaian hubung singkat tersebut. Arus ini disebut dengan Arus Norton (I_N).Kita telah melakukan hubungsingkat (short) terminal AB untuk mendapatkan Arus Norton (I_N) sehingga Resistor 60Ω dan 30Ω menjadi terhubung secara paralel. Kedua resistor tersebut kemudian terhubung seri terhadap resistor 20Ω.
Dengan demikian Total Resistansi (Rt) yang akan terhubung ke Sumber adalah sebagai berikut :

Rt = 20Ω + (60Ω || 30Ω) ⇒ (yang dimaksud dengan “||” adalah Paralel )
Rt = 20Ω + ((30Ω x 60Ω) / (30Ω + 60Ω))
Rt = 20Ω + 20Ω
Rt = 40Ω

Setelah mendapatkan nilai Total Resistor (Rt), maka selanjutnya adalah menghitungkan Arus listrik yang mengalir dengan menggunakan Hukum Ohm :
Baca juga : Pengertian dan Rumus Hukum Ohm.

It = V / Rt
It = 12V / 40Ω
It = 0,3A

Kemudian carikan nilai arus sumber (I_Sc) yang juga sama dengan nilai arus Norton (I_N) dengan menggunakan prinsip Pembagi Arus (Current Divider Rule).

I_Sc = I_N = 0,3A ((60Ω / (30Ω + 60Ω))
I_Sc = I_N = 0,2A

Jadi Arus Norton adalah 0,2A.

Langkah 3.

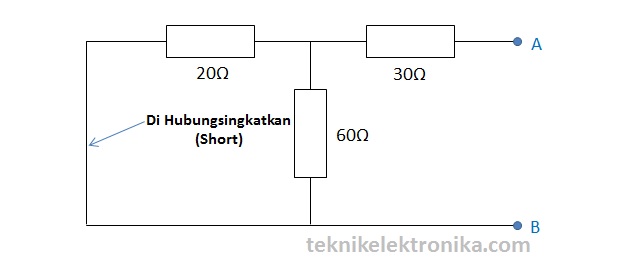
Lepaskan Arus Sumbernya, Short atau Hubungsingkatkan Tegangan Sumber dan lepaskan Resistor Beban seperti pada gambar dibawah ini :

Langkah 4.

Hitung atau ukur Resistansi Rangkaian Terbuka. Resistansi ini dinamakan dengan Resistansi Norton (R_N).
Karena Tegangan sumber dihubungsingkatkan pada langkah 3,  maka tegangan sumbernya sama dengan 0. Seperti pada gambar, kita dapat melihat Resistor 30Ω adalah berhubungan Seri dengan Resistor 60Ω dan 20Ω. Perhitungan untuk mencari Resistor Norton (R_N) adalah sebagai berikut :

R_N = 30Ω + (60Ω || 20Ω)) ⇒ (yang dimaksud dengan “||” adalah Paralel )
R_N = 30Ω + ((60Ω x 20Ω) / (60Ω + 20Ω))
R_N = 30Ω + 15Ω
R_N = 45Ω

Jadi, Nilai Resistor Norton (R_N) adalah 45Ω.

Langkah 5.

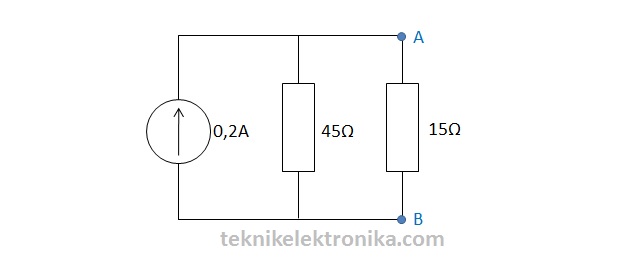
Hubungkan Resistor Norton (R_N) secara paralel dengan sumber arus (I_N) dan pasangkan kembali Resistor beban seperti pada gambar dibawah ini :

Langkah 6.

Langkah terakhir adalah menghitung nilai arus beban dan nilai tegangan beban pada Resitor beban berdasarkan Hukum Ohm :

Menghitung Arus Beban (I_L) yang mengalir melalui Resistor beban (R_L)

I_L = IN x ((RN / (RN + R_L))
I_L = 0,2A x ((45Ω / ((45Ω + 15Ω))
I_L = 0,15A

Dan

Menghitung Tegangan Beban (V_L) pada Resistor Beban (R_L)

V_L = I_L x R_L
V_L = 0,15A x 15Ω
V_L = 2,25V

Jadi Arus Beban yang mengalir melalui Resistor Beban adalah 0,15A, sedangkan Tegangan bebannya adalah 2,25V.

 

Dari Rangkaian aslinya sampai ke Rangkaian Ekivalen Norton, kita dapat melihat perbedaan yang sangat besar, rangkaian Ekivalen Norton lebih sederhana dan lebih mudah untuk merangkainya.