Sistem Bilangan pada Elektronika Digital – Bilangan adalah objek matematika yang digunakan untuk pengukuran, penghitungan dan pelabelan. Sedangkan yang dimaksud dengan Sistem Bilangan adalah sistem penulisan yang digunakan untuk mengekspresikan bilangan. Sistem Bilangan juga dapat didefinisikan sebagai cara yang digunakan untuk mewakili besaran suatu item fisik. Setiap sistem bilangan menggunakan bilangan dasar atau basis tertentu yang dalam bahasa Inggris biasanya disebut dengan “Base” atau “Radix”. Dalam pengertiannya, Base atau Radix dari sistem bilangan adalah jumlah total digit atau jumlah suku angka yang digunakan dalam suatu sistem bilangan. Contohnya pada sistem bilangan Desimal, Radix dari sistem bilangan Desimal adalah 10, yang artinya adalah memiliki 10 suku angka yakni 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Sistem Bilangan pada Elektronika Digital
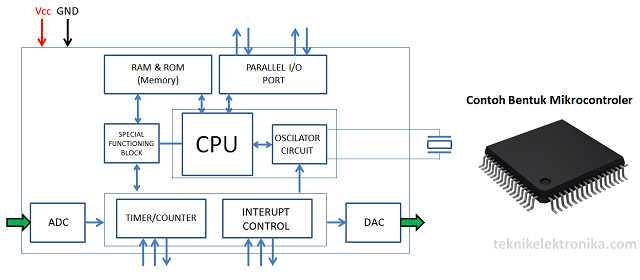
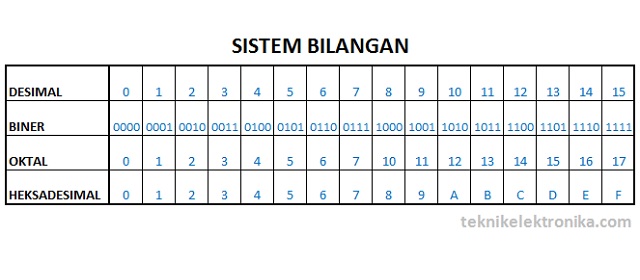
Dalam dunia Elektronika Digital, Pengetahuan Sistem Bilangan merupakan pengetahuan dasar yang wajib dipelajari, karena semua rangkaian digital yang dirancang ataupun perangkat digital menggunakan konsep sistem bilangan tersebut. Sistem Bilangan dalam elektronika digital digunakan untuk mewakili informasi yang akan diolah ataupun pemrosesan hingga hasil olahannya. Sistem Bilangan yang umumnya digunakan dalam teknik elektronika digital diantaranya adalah Sistem Bilangan Desimal, Biner, Heksadesimal dan Oktal.
Sistem Bilangan Desimal (Decimal)
Basis atau Radix dari sistem bilangan Desimal ini adalah 10 yaitu berkisar dari angka 0 hingga 9 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Digit atau angka yang terletak di sebelah kiri koma desimal disebut dengan bilangan bulat sedangkan digit atau angka yang terletak di sebelah kanan titik desimal disebut dengan bilangan pecahan. Sistem Bilangan Desimal ini merupakan sistem bilangan yang dipergunakan pada kehidupan kita sehari-hari. Perlu diketahui bahwa Indonesia menggunakan koma untuk menunjukan separator (pemisah) antara bilangan bulat dengan bilangan pecahan sedangkan negara-negara lainnya menggunakan tanda titik sebagai separator pecahannya.
Di sistem bilangan desimal ini, digit atau angka yang berada di posisi berturut-turut disebelah kiri koma desimal memiliki bobot 100, 101, 102, 103, 104 dan seterusnya. Sedangkan digit atau angka yang berada di posisi berturut-turut disebelah kanan koma desimal memiliki bobot 10-1, 10-2, 10-3, 10-4 dan seterusnya. Artinya, setiap posisi digit yang ditempati memiliki bobot masing-masing dengan pangkat bilangan yang berbasis 10.
Contoh :
Kita ambil contoh pada sebuah bilangan Desimal 235,12. Bagian bilangan bulatnya adalah 235 sedangkan bagian bilangan pecahannya adalah 0,12. Digit-digitnya 5, 3, dan 2 masing-masing memiliki bobot 102, 101 dan 100. Demikian juga digit 1 dan 2 dibelakang koma memiliki bobotnya masing-masing yaitu 10-1 dan 10-2.
Secara Matematis, dapat kita tulis sebagai berikut :
235,12 = (2 x 102) + (3 x 101) + (5 + 100) + (1 x 10-1) + (2 x 10-2)
Sistem Bilangan Biner (Binary)
Sistem Bilangan Biner atau Binary Numbering System adalah sistem bilangan yang berbasis dua dan merupakan sistem bilangan yang digunakan oleh semua rangkaian elektronika yang bersistem digital. Basis atau Radix dari sistem bilangan Biner ini adalah 2 yaitu angka 0 dan 1 saja. Di sistem bilangan Biner ini, setiap angka atau digit memiliki bobot 20, 21, 22, 23, 24 dan seterusnya.
Baca juga : Pengertian Aljabar Boolean dan Hukum Aljabar Boolean.
Contoh :
Sebagai contoh, kita gunakan bilangan Biner 10112. Ini berarti digit-digitnya yaitu 1, 0, 1 dan 1 memiliki bobot masing-masing 23, 22, 21 dan 20 (dihitung dari kanan ke kiri).
Secara Matematis, dapat kita tulis sebagai berikut :
10112 = (1 x 23) + (0 x 22) + (1 + 21) + (1 x 20)
Jika kita konversikan bilangan biner 10112 ke bilangan desimal akan menjadi 11.
Baca juga : Cara Konversi Bilangan Desimal ke Bilangan Biner.
Sistem Bilangan Oktal (Octal)
Sistem Bilangan Oktal atau Octal Numbering system adalah sistem bilangan yang berbasis delapan (8). Jadi, angka yang digunakan adalah berkisar diantara 0 hingga 7 (0, 1, 2, 3, 4, 5, 6, 7). Di sistem bilangan Oktal ini, masing-masing angka atau digit memiliki bobot 80, 81, 82, 83, 84 dan seterusnya.
Contoh :
Sebagai contoh, kita gunakan bilangan Oktal 72148. Ini berarti digit-digitnya yaitu 7, 2, 1 dan 4 memiliki bobot masing-masing 83, 82, 81 dan 80.
Secara Matematis, dapat kita tulis sebagai berikut :
72148 = (7 x 83) + (2 x 82) + (1 + 81) + (4 x 80)
Jika kita konversikan bilangan Oktal 72148 bilangan Desimal akan menjadi 3724.
Baca juga : Cara Konversi Bilangan Desimal ke Bilangan Oktal.
Sistem Bilangan Heksadesimal (Hexadecimal)
Sistem Bilangan Heksadesimal atau Hexadecimal Numbering System adalah sistem bilangan yang berbasis 16. Sistem Bilangan Heksadesimal ini menggunakan angka atau digit 0 hingga 9 dan huruf A sampai F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Huruf A hingga F ekivalen dengan 10 hingga 16. Jadi, pada dasarnya sistem bilangan Heksadesimal ini merupakan gabungan angka dan huruf. Di sistem bilangan Heksadesimal ini, masing-masing angka atau digit memiliki bobot 160, 161, 162, 163, 164 dan seterusnya.
Contoh :
Sebagai contoh, kita gunakan bilangan Oktal 7A1C16. Ini berarti digit-digitnya yaitu 7, A, 1 dan C memiliki bobot masing-masing 163, 162, 161 dan 160.
Secara Matematis, dapat kita tulis sebagai berikut :
7A1C16 = (7 x 163) + (10 x 162) + (1 + 161) + (2 x 160)
Jika kita konversikan bilangan Heksadesimal 7A1C16 ke bilangan Desimal akan menjadi 31260.